画面サイズ（横：/縦：）

２都市間の距離を求める(オールＰＨＰ版)へ

地球上の２地点間の距離計算の方法 （誤差が若干出るので研究中です）

（１）２つの都市が同じ半球にある場合

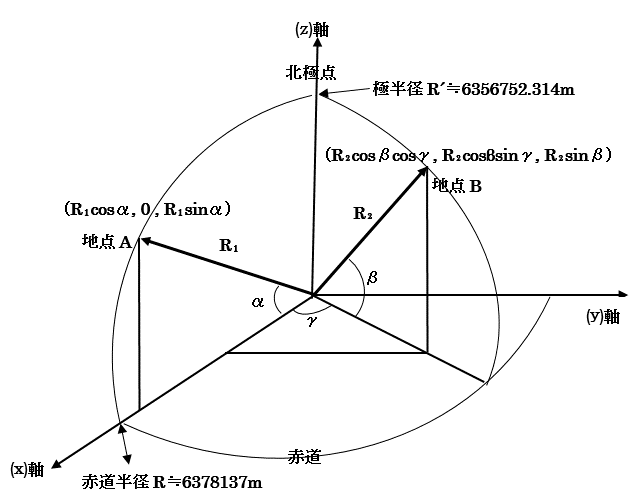
【図１】

上の図１において、地点Ａの緯度をα°, 地点Ｂの緯度をβ°, ２地点間の経度の差をγ°とすれば ,２つの空間ベクトル のなす角をθとすれば ちょっと！待ったー！ （↑）ナンでこうなるの？教えてよ～！→ 三角比を用いて詳しく説明します。 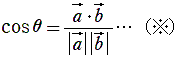だから だけを求めればよい。なぜかと言うと となる。上の図１で確認してね！

地点Ａと地点Ｂにおける地球の半径は「 その地点における緯度 」を用いて求められる。緯度が高くなればなるほど地球の半径は少しずつ短くなる。 下の図２で説明します。 【図２】 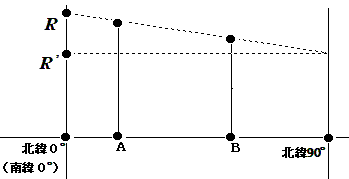上の図２において、地点Ａの緯度を北緯α°(←アルファ) 、地点Ｂの緯度を北緯β°とすれば、地点Ａにおける地球の半径は Ｒ1＝Ｒ－α×（Ｒ－Ｒ’）÷90で求められます。その証拠にα＝０のときはＲ1＝Ｒとなり、α＝90のときは Ｒ1＝Ｒ’となります。 また、緯度が45°のときは、 Ｒ1＝Ｒ－45×（Ｒ－Ｒ’）÷90＝（Ｒ＋Ｒ’）÷２なので、ＲとＲ’の平均になります。 ※表記の都合上「Ｒ（下付き小文字１）」をＲ1と表しています。 （完全数式通りに表記することも可能ですが面倒なので・・・） となる。上の式（※）に（１）の値を代入すれば、 となります。（↑）上の式を 【式（１）】 とおこう！ 上の【式（１）】の値がわかれば、２つの空間ベクトルのなす角θがわかります。 cosθから角度θを求めるには逆関数の「アークコサイン関数」を用います。 「アークコサイン」とは、y=cosθからθを求める関数のことでθ=arccos(y)で求められます。 角度θは、0 (ゼロ) ～ π（パイ） の範囲内のラジアン（弧度法）です。 さて、なす角θがわかったら次は下の【図４】で説明します。 図の赤い部分が求める距離ですが、赤い部分は楕円上にあるので、計算が面倒になります。 そこで、計算を楽にする方法として次の２つの方法が考えられます。

※ 【図４】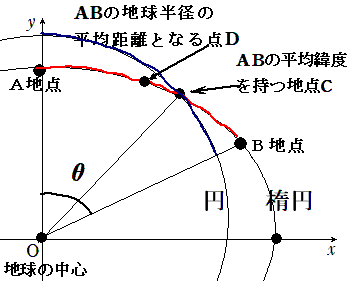 【第１の方法】 　若干の誤差が出ますが、２地点ＡＢのそれぞれの緯度の平均緯度を求めて（上の図の点Ｃ）、その「 平均緯度における地球の半径 」での円周を求めてから２地点間の距離の近似値を求める方法 【第２の方法】 　これもある程度の誤差が出ますが、２地点ＡＢでのそれぞれの「地球の半径」を求めて、その「 地球半径の平均での円周 」を求めてから２地点間の距離の近似値を求める方法（上の図の点Ｄ） 【第３の方法】 　これもある程度の誤差が出ますが、２地点ＡＢを通る楕円（上の図の赤い部分が乗っている楕円）の方程式を求めて「 ｎ等分に区分して」それぞれの微小幅での距離を三平方の定理を用いて計算して、 それらを合算することによって「２地点間の距離の近似値」を求める方法 【第４の方法】 もっとも誤差がすくない方法は「 楕円積分を用いる方法 」でしょうが、今後の研究課題としておき、ここでは「第１～第３の方法」で計算します。

２都市間の距離を求める(オールＰＨＰ版)へ

（２）赤道をはさんで南半球と北半球にある場合

【図５】

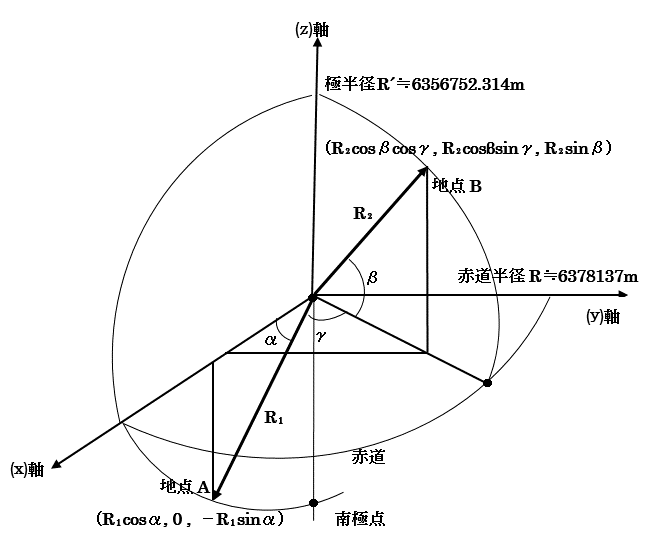上の図５のように２つの都市が赤道をはさんで南北の半球にある場合

三角比の基礎を用いて説明するよ！

【図６】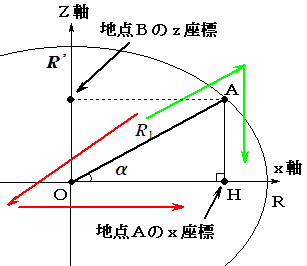 上の【図６】で説明するよ！ 三角比の定義に従えば、 cosα＝（底辺）／（斜辺）＝ＯＨ／Ｒ1　だから (↑)(↓)コサインアルファ cosα＝（地点Ａのｘ座標）／Ｒ1　となり、地点Ａのｘ座標＝Ｒ1cosα　と表せます。 また、sinα＝（対辺）／（斜辺）＝ＡＨ／Ｒ1　だから sinα＝（地点ＡのＺ座標）／Ｒ1　となり、地点ＡのＺ座標＝Ｒ1sinα　と表せます。 よって、点Ａの座標は（Ｒ1cosα , 0 , Ｒ1sinα） となります。 次は「ちょっと（かなり？）ややこしい」けど、点Ｂの座標の求め方を説明します。 もどる

２都市間の距離を求める(オールＰＨＰ版)へ